05. Finding the Lines: Search from Prior
Skip the sliding windows step once you've found the lines
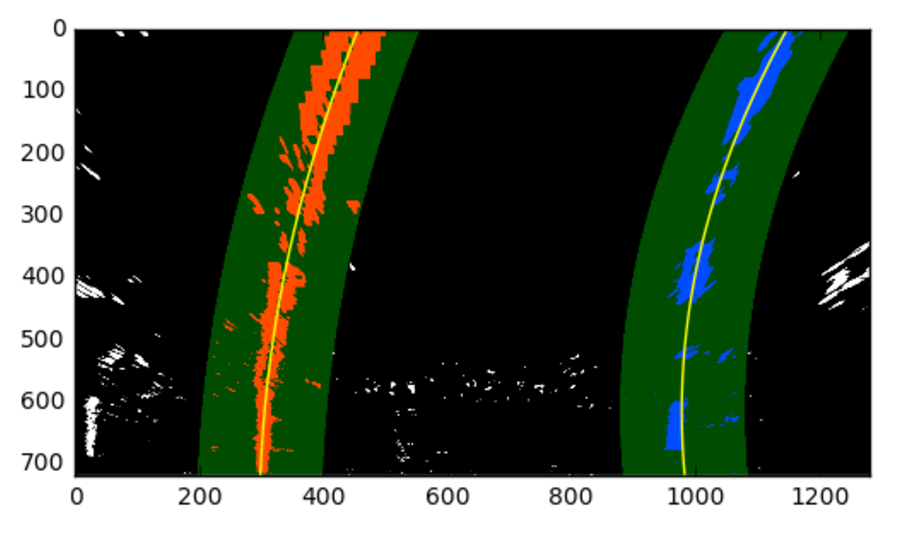
Great work! You've now built an algorithm that uses sliding windows to track the lane lines out into the distance. However, using the full algorithm from before and starting fresh on every frame may seem inefficient, as the lane lines don't necessarily move a lot from frame to frame.
In the next frame of video you don't need to do a blind search again, but instead you can just search in a margin around the previous lane line position, like in the above image. The green shaded area shows where we searched for the lines this time. So, once you know where the lines are in one frame of video, you can do a highly targeted search for them in the next frame.
This is equivalent to using a customized region of interest for each frame of video, and should help you track the lanes through sharp curves and tricky conditions. If you lose track of the lines, go back to your sliding windows search or other method to rediscover them.
Let's walk through one way to do this, and then you'll build it out further in a quiz below.
Use the previous polynomial to skip the sliding window
In the previous quiz, we used
left_lane_inds
and
right_lane_inds
to hold the pixel values contained within the boundaries of a given sliding window. This time, we'll take the polynomial functions we fit before (
left_fit
and
right_fit
), along with a hyperparameter
margin
, to determine which activated pixels fall into the green shaded areas from the above image. Note that this
margin
can be a different value than the one originally used for your sliding windows!
To implement this in the below quiz, you'll want to grab only those pixels with x-values that are +/- your
margin
from your polynomial lines. Note that you'll only need to implement
left_lane_inds
and
right_lane_inds
in the quiz - most of the surrounding code, ignoring iterating through the windows, is the same as before!
The way we'll visualize this is a bit different than last time around, however, so make sure to pay attention to that if you want to visualize this step while working on your project.
Quiz
In the below quiz, implement the following (see
TO-DO
's):
-
Fit a polynomial to all the relevant pixels you've found in your sliding windows in
fit_poly(). -
Set the area to search for activated pixels based on
marginout from your fit polynomial withinsearch_around_poly. Note that the quiz grader expects amarginof100pixels, but you can tune this as part of your own project!
Start Quiz:
Fitting on Large Curves
One thing to consider in our current implementation of sliding window search is what happens when we arrive at the left or right edge of an image, such as when there is a large curve on the road ahead. If
minpix
is not achieved (i.e. the curve ran off the image), the starting position of our next window doesn't change, so it is just positioned directly above the previous window. This will repeat for however many windows are left in
nwindows
, stacking the sliding windows vertically against the side of the image, and likely leading to an imperfect polynomial fit.
Can you think of a way to solve this issue? If you want to tackle the curves on the harder challenge video as part of the project, you might want to include this in your lane finding algorithm.